Geography lesson. Alice is asked to list all neighbour countries of Switzerland. Alice is a smart girl and she responds: “Germany, France, Austria and Italy”. Few years after Alice goes to the University to study Computer Science. She receives similar question.

How to store political map of the World (where each country is represented by a polygon) in a way to be able to efficiently perform the following operations:

  • Given a country be able to draw this country contour
  • Given a country be able to tell all it’s neighbours
  • Given a coordinate be able to tell which country are you in

Little bit of library research, and Alice exclaims “Eureka!” and notes “DCEL” in her little black notebook.

DCEL fully satisfied Alices requirements and is useful in many other situation where we should store planar subdivisions.

Linked list and doubly linked list

For better understanding what is DCEL, let’s have a little recap and recall what is linked list and doubly linked list.

A linked list is a linear data structure where each element is a separate object. Linked list elements are linked using pointers. Unlike an Array, linked list is not stored as contiguos location. Linked list node cannot be accessed by index (it is not random access collection)

Linked list consists of nodes. Each node holds the data and the reference to the next node.

The last node has a reference to null. The reference to the first node is called head. Empty linked list is a reference to null. Last element of the linked list holds reference to null (tail).

To find an element in linked list you start from the head and follow references to the next until your requirement is satisfied or you reach the last element. To iterate through all elements you can use while loop until the reference to the next pointer will be null.

Doubly linked list (DLL) is very similar to the Linked list except one crucial difference. Each element of Doubly linked list holds the data and two references. One to the next element and another to the previous element. First element of DLL holds reference to next and null (because it has no previous node). Last element vice versa.

Doubly linked list is convenient data structure to store polygon (each linked list node represents a Point. previous and next are holding references to the previous and next vertex in selected order. Usually Counter Clockwise (CCW).

The anatomy of DCEL

fig_1

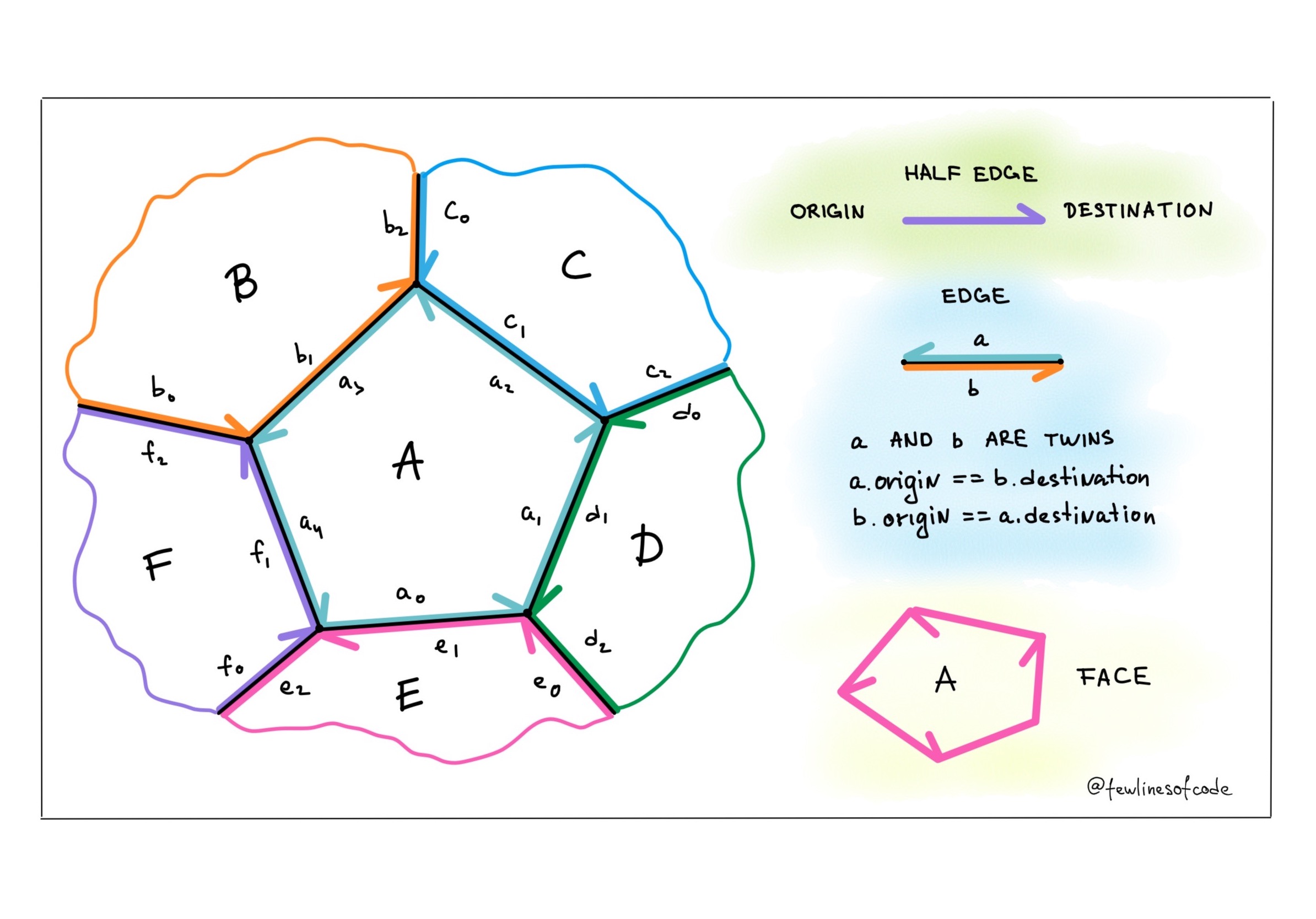
A doubly-connected edge list contains a record for each Face, Edge and Vertex of the subdivision.

Pseudocode:

DCEL
    var vertices: [Vertex]
    var halfEdges: [HalfEdge]
    var faces: [Face]

Vertex stores the coordinates of the point (x, y) and the pointer to incidentHalfEdge (HalfEdge originating in this point)

Pseudocode:

Vertex
	var x, y: Numeric
	var incidentHalfEdge: HalfEdge

Half edge Holds references to it’s prev and next - Inorder elements in a doubly connected linked list, reference to the twin and to the incidentFace. We will discuss twin and incident face a bit later. There is no point to store destination as it can be taken from twin origin. Yet you can do it if you want :).

Pseudocode:

HalfEdge
	var incidentFace: Face
	var twin: HalfEdge
	var prev: HalfEdge
	var next: HalfEdge 
	
	GetDestination() -> HalfEdge 
	  return next.origin
  
  	GetOrigin() -> HalfEdge 
	  return prev.destination

Edge is formed by two Half edges called twins.

In DCEL, half edges ${a}$ and ${b}$ are twins when:

  • They hold a pointer twin to each other
  • origin of ${a}$ is a destination of ${b}$ and vice versa.

Two twin half edges form an Edge.

Edge is not explicitly defined in the DCEL data structure.

Face models closed (in most cases) region represented by Doubly linked list of half edges. Face holds the reference to the arbitrary half edge. Half edges of the Face are organised into looped Doubly linked list. In looped doubly linked list last element holds the reference to the firs and vice versa. You can iterate through half edges both ways. Each element can be visited. Be careful! It is very easy to create an infinite loop! Also keep an eye on memory leaks.

Pseudocode:

Face
	var incidentHalfEdge: HalfEdge // Doubly linked list

Each of the DCEL elements can hold one more reference to the satellite data of any kind. For instance – color, population number or anything else.

Some common operations on DCEL

  • Visit all vertices for a given Face (often called Face Hull)
  • Visit all edges for a given Face
  • Find all neighbours of a given Face (this is how Alice solved her problem)

And many more. Given a DCEL implementation it is fairly easy to implement basic operations.

Conclusion

DCEL without any additional operations is literally a way of data organization. It is fairly simple data structure, yet it is fundamental if you are trying to work with Planar subdivisions.

It is also worth of saying that you can modify it for the sake of convenience and sacrifice a very little of memory resources.

If you will follow me on twitter @fewlinesofcode and read next articles in Fortunes Algorithm series, you will see the simple power of DCEL.

Swift code and Homework

Here is a naive DCEL implementation in Swift:

public class Vertex {
    private(set) var x: Double
    private(set) var y: Double
    
    private(set) var incidentEdge: HalfEdge?
    
    public init(x: Double, y: Double) {
        self.x = x
        self.y = y
    }
}

public class Face {
    private(set) var origin: HalfEdge? = nil
}

public class HalfEdge {
    private(set) var origin: Vertex
    var twin: HalfEdge?
    var face: Face?
    var prev: HalfEdge?
    var next: HalfEdge?
}

public class DCEL {
    private(set) var vertices: [Vertex] = []
    private(set) var halfEdges: [HalfEdge] = []
    private(set) var faces: [Face] = []    
}

Homework for the curious ones:

  1. Name faces, edges, half edges as it is on the image
  2. Fix memory leaks

  3. Implement basic DCEL operations:

    • Visit all vertices for a given Face (often called Face Hull)
    • Visit all edges for a given Face
    • Find all neighbours of a given Face (this is how Alice solved her problem)
  4. This implementation uses reference types (classes). Can you reimplement it in Swift using value types (structs)?

The result of Fortunes algorithm is a Doubly Connected Edge List storing Voronoi diagram.

Where to go from here

This article is based on the third edition of amazing book “Computational Geometry. Algorithms and applications” by Mark de Berg, Otfried Cheong, Marc van Kreveld and Mark Overmars.

I highly recommend this book for reading.